

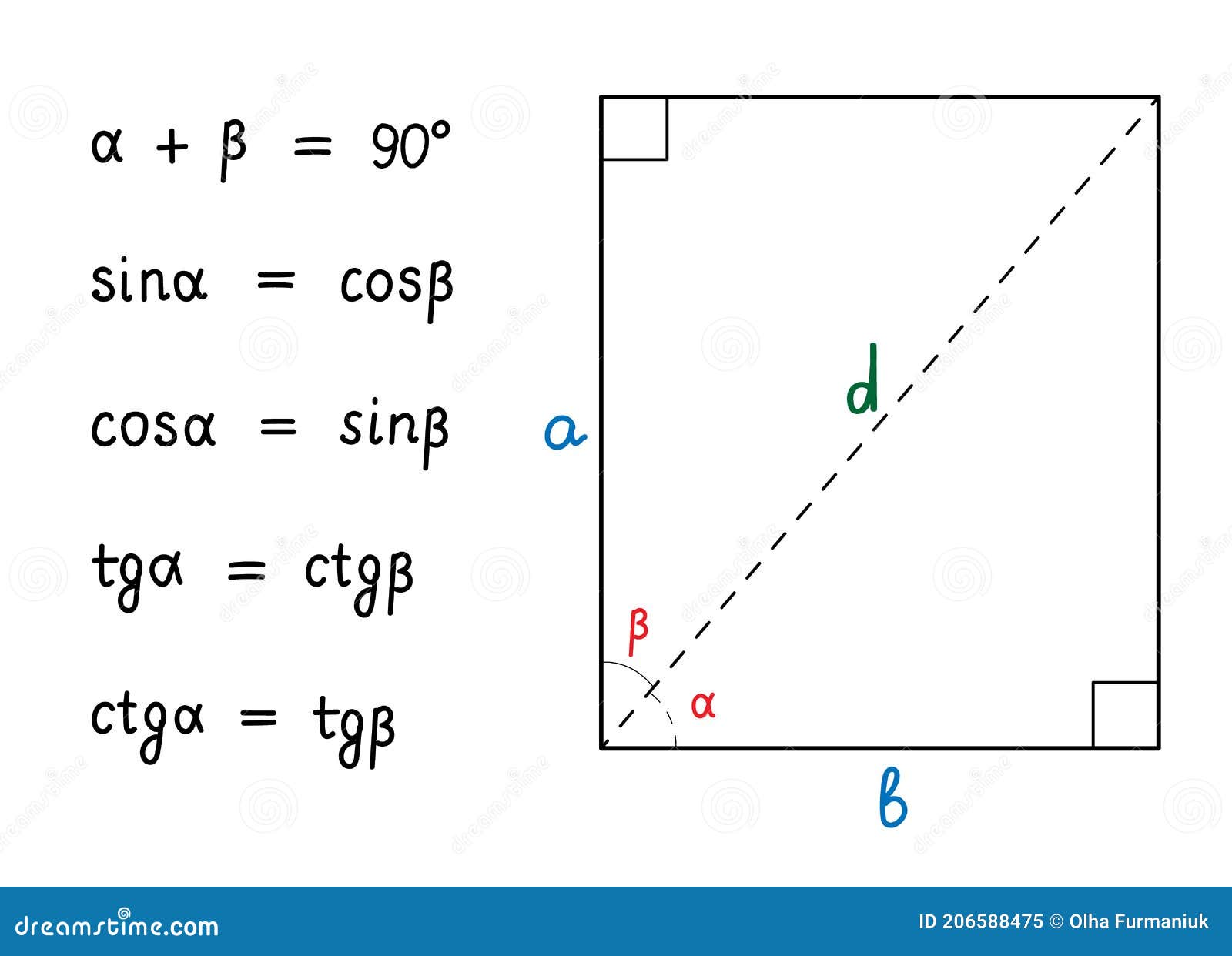
Just like breaking apart $17^2$, let’s multiply out the pieces: Aha! We can use Euler’s Formula to draw the rotation we need: Now here’s the weird thing: I can draw what the new height should be ( It’s right there!), but I can’t turn my drawing into an equation.Įuler’s Formula lets us create a circular path using complex numbers:Ĭrucially, multiplying complex numbers performs a rotation. The relationship between angle and height can’t be simple addition. If we keep adding up angles, their height increases until the max (100%), then starts decreasing. Remembering that sine is “height (as a percentage of max)”, this equation asks: If we add two angles, what is their total height?Ī quick guess might be to combine the individual heights: This is useful in factoring, simplifying equations, and so on. The important aspect is realizing that $(a + b)^2$ can be broken into simpler ingredients: $a^2, b^2, a, b$. In the computer era, sure, we can just crunch $17^2$ directly. Working out $17^2$ directly is cumbersome. In algebra, we study relationships like this: Instead of memorizing these bad mamma jammas, let’s learn to draw the formulas. In math terms, we’re looking for formulas like this ( full cheatsheet): Starting from the Pythagorean Theorem and similar triangles, we can find connections between sin, cos, tan and friends ( read the article on trig).Ĭan we go deeper? Maybe we can connect sine with itself (sin-ception).
#Trigonometric identities formulas tan how to#
Trig identities are notoriously difficult to memorize: here’s how to learn them without losing your mind.


 0 kommentar(er)
0 kommentar(er)
